Équilibre de Nash
L'équilibre de Nash désigne une situation où chaque joueur choisit la meilleure stratégie possible (stratégie dominante) en fonction de ses anticipations concernant le choix de l'autre joueur. Il s'agit d'un ensemble de choix (m1, m2) où chaque décision représente la meilleure réponse à l'action de l'autre. Les joueurs forment des suppositions sur les choix de leurs adversaires et adaptent leur propre stratégie en conséquence (« faire ce qui est le mieux pour soi-même et pour les autres »). Un équilibre de Nash est stable, car aucun joueur n'a intérêt à modifier sa stratégie (stratégie). Chaque joueur maximise son propre gain en prenant en compte la meilleure décision de l'autre. Toute déviation entraînerait une détérioration de sa situation (gain / utilité). L'équilibre de Nash représente un état optimal dans un jeu non coopératif et est donc aussi appelé équilibre non coopératif. Cet équilibre n'est pas le résultat d'un accord entre les joueurs, mais émerge naturellement lorsque chacun adopte des stratégies dominantes qui garantissent le meilleur résultat individuel et un équilibre collectif optimal. La matrice de gains suivante illustre un équilibre de Nash dans un jeu non coopératif à deux joueurs. Bien que cet exemple porte sur deux joueurs, le concept peut s'étendre à un nombre N de joueurs.
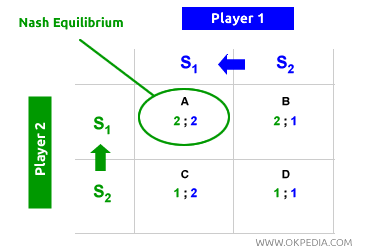
Dans la matrice, chaque joueur peut opter pour la stratégie S1 ou S2. Le joueur 1 prévoit que le joueur 2 choisira S1 (sa stratégie dominante), et choisit donc également S1, car cela lui rapporte un gain individuel de 2. De la même manière, le joueur 2 anticipe le choix de S1 par le joueur 1 et adopte lui aussi S1. L'équilibre du jeu se fixe donc dans la case A de la matrice (en haut à gauche), où les deux joueurs maximisent leurs gains individuels (optimum individuel) en choisissant leurs stratégies dominantes (équilibre de Nash). Les deux joueurs anticipent le mouvement optimal (stratégie dominante) de leur adversaire et choisissent leurs stratégies dominantes en conséquence. L'exemple suivant aide à clarifier le processus décisionnel derrière l'équilibre de Nash.
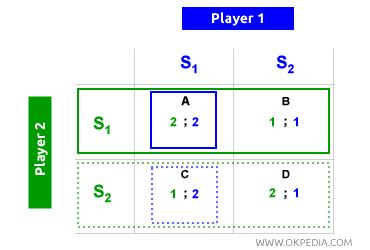
Le joueur 1 (vert) peut choisir S1 ou S2, mais dans les deux cas, il cherche à obtenir le gain maximal (2) dans les cases A et D. Cependant, il sait que s'il choisit S2, le joueur 2 (bleu) répondra avec S1, et l'équilibre sera atteint dans la case C, où son gain est minimal (1). En choisissant S1, le joueur 1 sait que le joueur 2 fera de même, aboutissant ainsi à un équilibre dans la case A, où le gain est maximal (2). En suivant la même logique, lorsque le joueur 2 est celui qui choisit en premier, il reconnaît que sélectionner S1 incitera également le joueur 1 à opter pour S1, fixant de nouveau l'équilibre dans la case A. La case A représente l'équilibre de Nash, tandis que les autres cases ne le sont pas. En résumé, l'équilibre de Nash est souvent décrit comme : « Gagner en faisant ce qui est le mieux pour soi-même et pour les autres ». C'est un concept fondamental de la théorie des jeux et de l'économie politique.
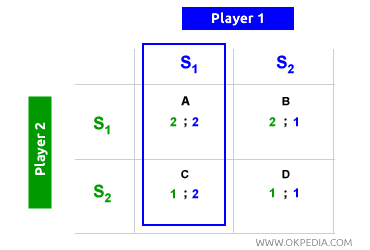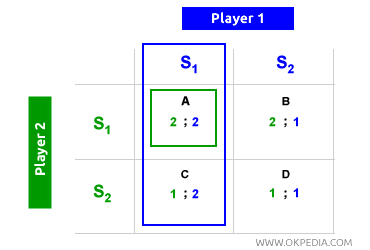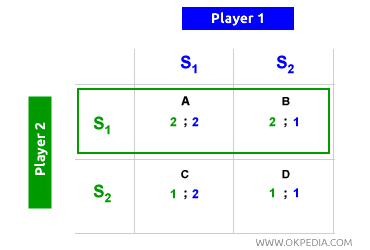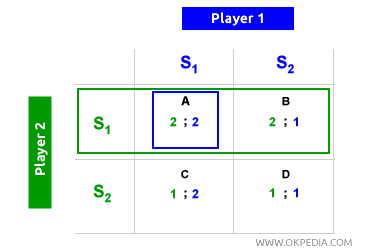
Optimum social. Dans un équilibre de Nash, il est possible d'atteindre un résultat optimal à la fois pour les deux joueurs et pour la société dans son ensemble. Par exemple, lorsque le joueur 1 (vert) choisit S1, le joueur 2 (bleu) suit en optant pour S1, ce qui conduit à un équilibre dans la case A. Lorsque le joueur 2 (bleu) choisit en premier S1, le joueur 1 (vert) choisit également S1, menant de nouveau à la case A. Ainsi, la case A est un équilibre de Nash. Dans ce cas, les deux joueurs reçoivent un gain de 2 (optimum individuel), et les gains combinés (2+2) donnent un total de 4 (optimum social). Par conséquent, dans la case A (équilibre de Nash), il existe à la fois un optimum individuel et social.
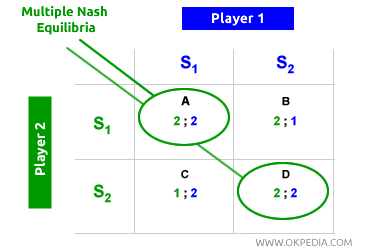
Multiples équilibres de Nash. Un jeu non coopératif peut comporter plusieurs équilibres de Nash. Même lorsque plusieurs équilibres existent, chacun reste stable, car toute déviation aggraverait le résultat pour chaque joueur. Par exemple, la matrice de gains suivante montre deux équilibres de Nash symétriques.
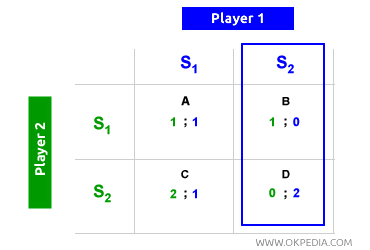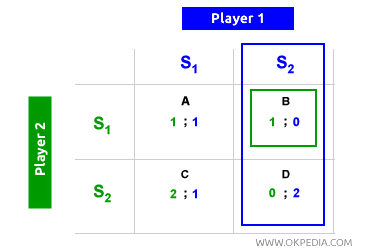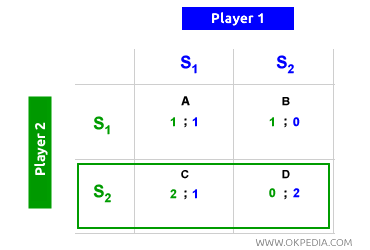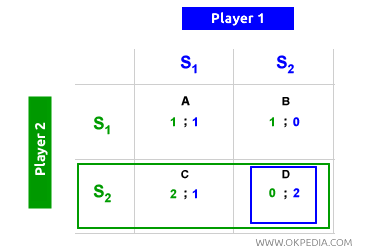
Absence d'équilibre de Nash. Un autre problème lié à l'équilibre de Nash est qu'il n'est pas toujours présent. De nombreux jeux ne comportent pas d'équilibre de Nash. Dans l'exemple ci-dessous, aucun équilibre de Nash n'existe. Lorsque le joueur 1 choisit S2, le joueur 2 opte pour S2, plaçant l'équilibre dans la case D. Inversement, lorsque le joueur 2 choisit S2, le joueur 1 choisit S1, déplaçant l'équilibre dans la case B. Il n'y a donc pas d'équilibre de Nash dans ce jeu.
Dilemme du prisonnier. Adopter des stratégies dominantes ne conduit pas toujours à un équilibre socialement optimal. En l'absence d'informations suffisantes, un jeu non coopératif peut aboutir à un équilibre stable mais sous-optimal. C'est ce qui est illustré dans le « dilemme du prisonnier », où deux joueurs, même en anticipant rationnellement les choix de l'autre et en optant pour des stratégies dominantes, se retrouvent dans un équilibre sous-optimal (D), aussi bien sur le plan individuel que collectif. L'équilibre D est un équilibre de Nash, mais ce n'est pas un optimum de Pareto. En conclusion, l'équilibre de Nash et l'optimum de Pareto diffèrent, car ils se fondent sur des conditions distinctes.
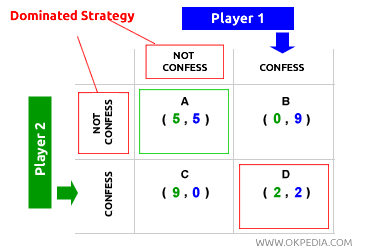
Par exemple, le joueur 1 s'attend à ce que le joueur 2 avoue, car avouer est la stratégie dominante de ce dernier. En avouant, le joueur 2 obtient sa liberté (gain de 9). Compte tenu de cette attente, le joueur 1 choisit l'option dominante entre B et D, décidant d'avouer également pour s'assurer un gain d'au moins 2. Le joueur 2 applique la même logique mais à l'inverse. L'équilibre D est un équilibre de Nash et reste stable, car aucun joueur n'a intérêt à changer de décision. Cependant, l'équilibre D n'est pas un optimum de Pareto, car les deux joueurs reçoivent un gain inférieur (2) comparé au gain plus élevé (5) qu'ils obtiendraient en choisissant tous deux de ne pas avouer (équilibre A).
Équilibre de Cournot. L'équilibre de Nash est un concept théorique d'équilibre similaire à celui de Cournot. Dans un duopole de Cournot, chaque entreprise choisit son niveau de production optimal en fonction de la décision stratégique de l'autre entreprise.
