Variable aléatoire
Une variable aléatoire modélise les résultats possibles d’un phénomène incertain, susceptibles de varier au sein d’un certain ensemble de valeurs. On parle également de variable stochastique ou, plus simplement, de variable aléatoire (souvent abrégée en v.a.).
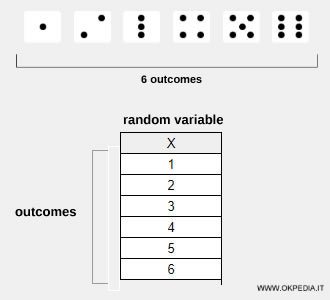
Exemple. La variable aléatoire X représente les issues {1, 2, 3, 4, 5, 6} d’un lancer de dé équilibré. Bien que l’on ne puisse pas prédire à l’avance la face obtenue, on sait qu’elle fera nécessairement partie des six résultats possibles de X.
En théorie des probabilités, une variable aléatoire constitue la formalisation mathématique d’un phénomène aléatoire, c’est-à-dire non déterministe.
Définition d’une variable aléatoire
Voici la définition formelle d’une variable aléatoire (ou stochastique) :
Étant donné un espace échantillonnal {Ω} composé de toutes les n-uplets issus d’une variable statistique K, et une mesure de probabilité P définie sur cet espace, une variable aléatoire X est une fonction mesurable allant de {Ω} vers un espace d’arrivée E.
Chaque élément de l’espace {Ω} est ainsi associé à une valeur unique que X peut prendre dans l’espace E.
Cette définition généralise celle proposée initialement par Lindgreen.
Définition de Lindgreen. Une fonction X définie sur l’espace {Ω} est dite mesurable par rapport à la σ-algèbre borélienne β si, pour tout réel λ, l’ensemble {ω ∈ Ω : X(ω) ≤ λ} appartient à β.
Types de variables aléatoires
Selon la nature du phénomène étudié, une variable aléatoire peut être classée comme suit :
- Variable aléatoire discrète
Lorsqu’elle prend ses valeurs dans un ensemble fini ou dénombrable. - Variable aléatoire continue
Lorsqu’elle peut prendre n’importe quelle valeur dans l’ensemble des réels ℝ.
Loi de probabilité
La loi de probabilité d’une variable aléatoire X est une fonction qui associe à chaque valeur possible de X sa probabilité P(X).
Exemple pratique
La variable aléatoire X modélise les résultats possibles obtenus en lançant un dé équilibré à six faces.
Chaque face a la même probabilité, soit P(X) = 1/6, ce qui correspond à 0,17 ou 17 %.
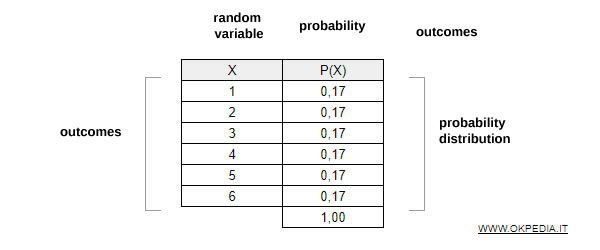
En attribuant une probabilité à chacune des issues possibles, on construit la loi de probabilité de la variable aléatoire.
La somme de toutes les probabilités de cette loi est toujours égale à 1.
Variables aléatoires univariées et multivariées
Les variables aléatoires peuvent également être classées en fonction de leur dimension :
- Variables aléatoires univariées : elles dépendent d’une seule variable ou dimension.
- Variables aléatoires multivariées (ou n-dimensionnelles) : elles prennent en compte deux dimensions ou plus.
Processus stochastiques
Un processus stochastique est une variable aléatoire dont les valeurs évoluent au cours du temps (t), le temps jouant ici le rôle de variable indépendante.
