Vecteurs
Les vecteurs sont des grandeurs définies à la fois par leur intensité et leur direction. Dans un espace à deux ou trois dimensions, un vecteur est représenté par une flèche de longueur déterminée, partant d'un point d'origine (O) et se terminant en un point (x, y).
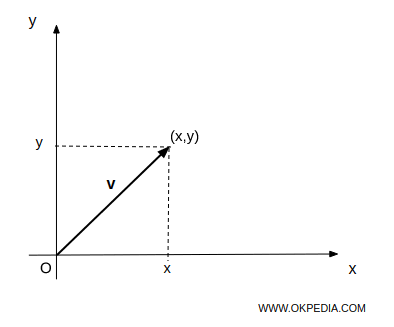
Un vecteur libre (ou simplement un vecteur) est un ensemble de segments orientés équivalents.
Deux ou plusieurs segments orientés sont considérés comme équivalents s'ils ont la même intensité, direction et orientation.
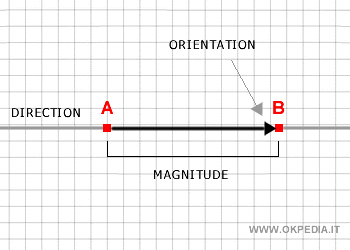
- Intensité : la longueur du vecteur. Elle est toujours positive et exprimée dans une unité de mesure spécifique.
- Direction : la ligne le long de laquelle se trouve le vecteur.
- Orientation : le sens du vecteur, indiqué par une flèche.
L'étude des vecteurs dans deux ou plusieurs dimensions fait partie du calcul vectoriel, une branche de l'algèbre linéaire qui s'intéresse aux grandeurs vectorielles.
Qu’est-ce qu’une grandeur vectorielle ? Une grandeur vectorielle est une grandeur qui peut être décrite par une intensité (longueur ou force), une direction et une orientation. Elle se distingue des grandeurs scalaires, qui sont des nombres réels associés à une unité de mesure.
Exemple de vecteur
Les segments orientés u, v et w appartiennent au même vecteur libre car ils ont la même direction, orientation et intensité (longueur).
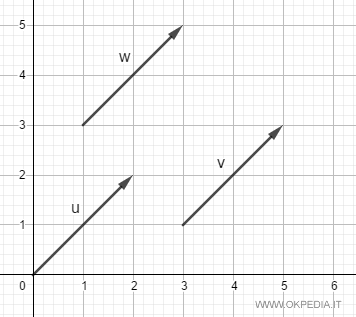
Ils font donc partie de la même classe d’équivalence.
La seule différence entre ces trois segments orientés réside dans leur point de départ.
Vecteur de position et vecteur de déplacement
Plusieurs notions sont associées aux vecteurs, notamment :
- Vecteur de position. Ce vecteur définit la position d'un point dans l'espace par rapport à un système de référence.
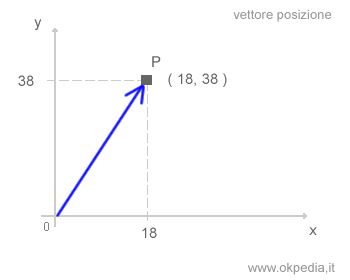
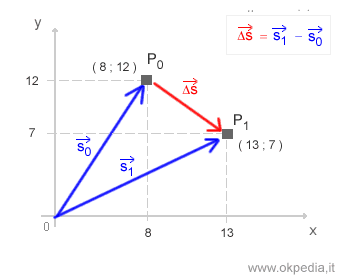
- Vecteur de déplacement. Représenté par une flèche allant de la position initiale d'un point à sa position finale, il illustre le changement de la position.
Opérations sur les vecteurs
Les vecteurs peuvent être soumis à diverses opérations telles que l'addition, la soustraction et la multiplication par un scalaire.
Chaque opération obéit à des règles et propriétés spécifiques qui déterminent l'intensité et la direction du vecteur résultant.
Les principales opérations impliquant des vecteurs sont :
- Addition de vecteurs
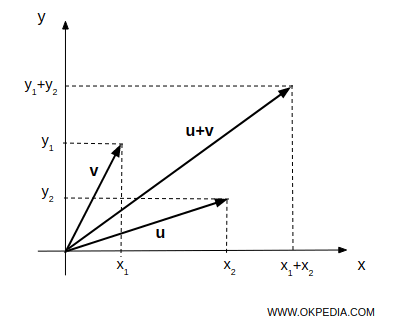
Si (x1, y1) et (x2, y2) sont les points d'extrémité de deux vecteurs, u et v respectivement, alors (x1 + x2, y1 + y2) est le point d'extrémité du vecteur u + v.
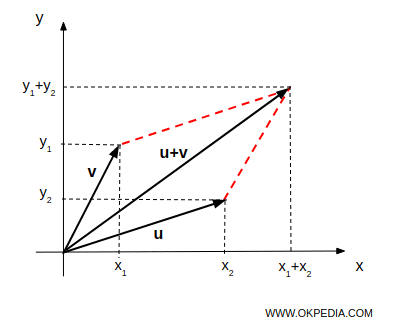
La somme de deux vecteurs dans l'espace R² = RxR peut également être obtenue à l'aide de la méthode du parallélogramme.
- Multiplication par un scalaire
Si (x, y) est le point d'extrémité du vecteur v, alors le produit kv donne un vecteur dont le point d'extrémité est (kx, ky).
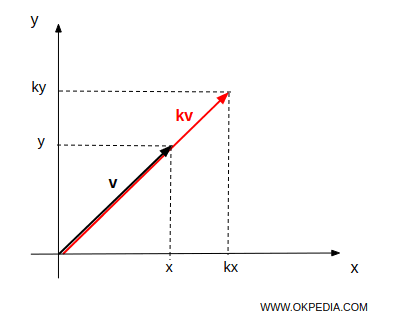
Le produit d'un nombre réel k et d'un vecteur v est obtenu en multipliant l'intensité de v par k. La direction reste inchangée si k > 0, ou est inversée si k < 0.
Vecteurs dans des dimensions supérieures
Un vecteur multidimensionnel est essentiellement une liste ordonnée de n valeurs, qui peut être considérée comme un n-uplet de nombres réels. Chaque valeur est représentée par un symbole avec un indice indiquant sa position dans la liste, comme x1, x2, ..., xn.
La notation des vecteurs utilise généralement une lettre surmontée d'une flèche, représentée comme suit :
$$ \vec{v} = (x_1, x_2, ..., x_n) $$
Les vecteurs sont essentiels pour décrire des grandeurs ne pouvant être représentées par une seule valeur. En physique, la force est un exemple classique de grandeur vectorielle.
Note. Sur Okpedia, les vecteurs sont différenciés des scalaires en les affichant en gras. Par exemple, u, w et v sont des vecteurs, tandis que u, v et w sont des scalaires.
