Équilibre walrasien

L'équilibre walrasien désigne un équilibre de marché dans un contexte de concurrence parfaite. Dans une économie composée de N marchés, un équilibre walrasien se produit lorsqu'un vecteur de prix P( p₁, ... , p_n ) parvient à égaliser l'offre S_n et la demande D_n sur chaque marché.

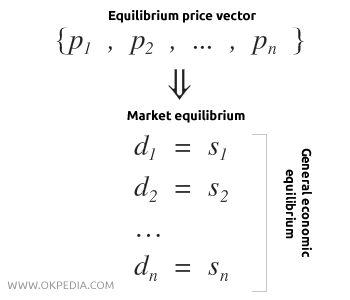
Lorsque tous les N marchés sont en équilibre, on parle alors d'équilibre économique général (EEG). Dans cette situation, la demande excédentaire (d_i-s_i) est nulle sur chaque marché, ce qui implique que la somme des excédents sur l'ensemble des marchés est également égale à zéro.

Chaque individu achète et vend exactement ce qu'il avait prévu.

L'équilibre walrasien détermine également les prix relatifs des biens, montrant que le rapport entre les prix (prix relatifs) reste constant, quel que soit le bien choisi comme numéraire.

Le modèle mathématique de Walras

Pour formaliser l'équilibre, Léon Walras a développé un modèle mathématique basé sur un système de deux ensembles d'équations.

1. Le premier ensemble d'équations garantit que l'offre et la demande s'égalisent pour chacun des N biens (équilibre de marché). Il y a donc autant de marchés qu'il y a de biens.
2. Le second ensemble exprime la quantité demandée (f_D) et la quantité offerte (f_S) de chaque bien en fonction de son prix de marché ( p_N ).

Les prix et les quantités demandées et offertes sont des variables interdépendantes. Le prix d'un bien influence sa demande et son offre, tandis que l'offre et la demande influencent à leur tour son prix de marché.

Le modèle de Walras représente une économie idéale où les individus achètent et vendent exactement comme ils l'avaient prévu.

Le processus de formation des prix dans ce modèle suit une approche par essais et erreurs appelée tâtonnement.

Tâtonnement

Le processus de tâtonnement s'apparente à une négociation collective, comme on peut l'observer lors des enchères publiques en bourse.

1. Un commissaire-priseur annonce un vecteur de prix P( p₁, ... , p_n ). Il s'agit de prix virtuels, c'est-à-dire qu'aucune transaction réelle n'a lieu à ce stade.
2. Sur la base de ce vecteur de prix, les agents économiques inscrivent sur un ticket la quantité demandée D( d₁, ... , d_n ) et la quantité offerte S( s₁, ... , s_n ) pour chacun des N biens.

   Walras adopte l'individualisme méthodologique propre aux économistes néoclassiques. Selon lui, chaque individu prend des décisions visant à maximiser son utilité personnelle. Ainsi, les quantités de biens qu'ils demandent ou offrent reflètent ce qu'ils estiment être dans leur meilleur intérêt.

3. Le commissaire-priseur collecte tous les tickets et totalise les quantités demandées et offertes pour chaque bien.
4. Si la demande et l'offre ( d_i=s_i ) sont égales pour chaque bien, l'enchère est conclue, le vecteur de prix devient officiel et les transactions réelles se font selon les quantités inscrites sur les tickets (équilibre économique général).

   S'il subsiste un excédent de demande ( d_i≠s_i ), le commissaire-priseur ajuste les prix sur les marchés en déséquilibre, annonce un nouveau vecteur de prix, et le processus recommence.

Dans l'équilibre économique général, chaque individu atteint le meilleur résultat possible en fonction des conditions du marché, car ils réalisent les transactions qu'ils avaient initialement prévues.

Dans le modèle de Walras, les décisions sont individuelles et les échanges sont volontaires. Il n'y a ni intermédiaires, ni organisations représentatives (comme des syndicats, des groupes de pression ou des cartels). Le marché ne sert qu'à la coordination des échanges.

Ainsi, si chaque individu maximise son utilité personnelle, le système économique dans son ensemble atteint un état optimal dans l'équilibre walrasien.

Optimalité de Pareto. L'équilibre walrasien en concurrence parfaite représente une allocation efficace au sens de Pareto (optimalité de Pareto). Le lien entre l'équilibre concurrentiel et l'efficacité de Pareto, à la fois en matière de consommation et de production, est établi dans le premier théorème fondamental du bien-être (théorèmes du bien-être).