Allocation optimale des facteurs
L'allocation optimale des facteurs désigne la combinaison des facteurs de production qui permet de minimiser les coûts tout en conservant le même niveau de production. Toute entreprise cherche à maximiser son efficacité en réduisant autant que possible ses coûts de production par rapport à ses revenus, tout en exploitant au mieux les technologies à sa disposition. L'allocation optimale des intrants peut être illustrée graphiquement à l'aide des droites d'iso-coût et des courbes d'isoquante. Une courbe d'isoquante représente l'ensemble des combinaisons d'intrants permettant d'obtenir un niveau de production identique, tandis qu'une droite d'iso-coût indique les combinaisons correspondant au même coût total. Sur un repère cartésien, les quantités des deux intrants, x1 et x2, sont représentées sur les axes.
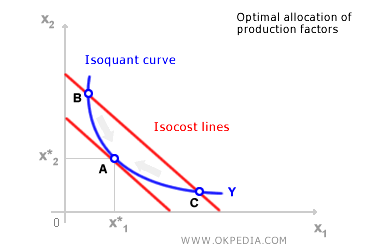
Le point d'allocation optimale correspond à l'intersection où la courbe d'isoquante est tangente à la droite d'iso-coût. Le point A représente le choix le plus efficient d'un point de vue économique (équilibre du producteur), car il minimise les coûts tout en maintenant la production au niveau Y. Tout autre point situé sur la courbe d'isoquante (comme B ou C) entraîne un coût de production plus élevé, car il se trouve sur une droite d'iso-coût plus coûteuse. Au point optimal A, la courbe d'isoquante et la droite d'iso-coût ont la même pente, ce qui signifie qu'elles sont tangentes. Cette tangence a une interprétation économique claire : à cet instant, le rapport des prix des intrants (- w1 / w2) est égal au taux marginal de substitution technique (TMST) entre les deux intrants x1 et x2.
- w1 / w2 = - TMST
Le taux marginal de substitution technique (TMST) correspond, à son tour, au rapport des productivités marginales des deux intrants :
TMST = - dx2 / dx1 = PM1 / PM2
Les prix relatifs des facteurs de production (- w1 / w2) sont fixés par le marché et échappent au contrôle des entreprises. En conséquence, la pente de la droite d'iso-coût est déterminée par les conditions du marché et ne peut être modifiée par les décisions d'une entreprise. Avec une technologie de production donnée, une entreprise cherche à optimiser sa production en atteignant la courbe d'isoquante la plus élevée possible (utilisation maximale des capacités) tout en minimisant ses coûts. Comme les prix des intrants déterminent la pente de la droite d'iso-coût, tout point situé sur l'isoquante en dehors de A incite l'entreprise à ajuster sa combinaison d'intrants : elle aura intérêt à utiliser davantage l'intrant offrant la plus forte productivité marginale et à réduire l'usage de celui dont la productivité marginale est plus faible. Ce réajustement permet de diminuer encore les coûts de production tout en maintenant le même niveau de production Y, améliorant ainsi l'efficacité. L'entreprise poursuivra ces ajustements jusqu'à atteindre le point de tangence, où le rapport des prix des intrants est égal au rapport de leurs productivités marginales. À ce stade d'allocation optimale, il n'existe plus de raison économique de modifier la combinaison des intrants.
