Isoquant

Un isoquant représente l'ensemble de toutes les combinaisons possibles de facteurs de production permettant d'obtenir un même niveau de production. Aussi appelées courbes d'isoquant, ces courbes jouent un rôle central en théorie économique, notamment dans l'étude de la production des entreprises. Le terme "isoquant" vient du grec "iso" (égal) et "quantité" (de production). Dans une fonction de production à deux facteurs, un isoquant peut être représenté dans un repère cartésien, où l'axe des abscisses indique la quantité du premier facteur (x₁) et l'axe des ordonnées représente la quantité du second facteur (x₂). Chaque point (x₁, x₂) du plan correspond à une combinaison spécifique d'intrants. La courbe d'isoquant relie toutes ces combinaisons qui produisent le même niveau de production (y), formant ainsi une courbe continue de production équivalente. Cette courbe est appelée courbe d'isoquant.

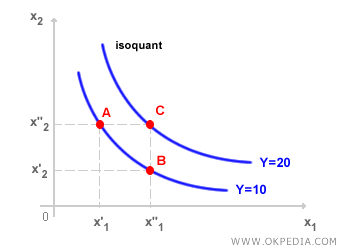
Chaque courbe d'isoquant correspond à un niveau de production différent. Les isoquants situés plus près de l'origine indiquent des niveaux de production plus faibles, tandis que ceux plus éloignés correspondent à des niveaux de production plus élevés. À l'instar des courbes d'indifférence en théorie du consommateur, les courbes d'isoquant sont décroissantes et convexes par rapport à l'origine. Cela traduit le principe selon lequel des combinaisons intermédiaires de facteurs sont souvent plus efficaces. Pour maintenir un même niveau de production en réduisant l'utilisation d'un facteur, il est nécessaire d'augmenter celle de l'autre. Le taux auquel un facteur peut être substitué à un autre tout en conservant le même niveau de production est appelé taux marginal de substitution technique (TMST). Ce taux se mesure par le rapport entre la variation d’un facteur (x₁) et la variation correspondante de l’autre facteur (x₂), tout en maintenant constant le niveau de production (y).