Isocoût

Un isocoût représente l’ensemble des combinaisons possibles de deux facteurs de production permettant d’atteindre un même coût de production. Pour un niveau donné des prix des facteurs (w₁/w₂), la droite d’isocoût indique quelles combinaisons de facteurs (x₁, x₂) peuvent être acquises tout en maintenant un coût total de production (C) constant. Graphiquement, l’équation de l’isocoût peut être représentée dans un repère cartésien. Dans les cas les plus simples, elle prend la forme d’une droite (droite d’isocoût), tandis que dans des configurations plus complexes, elle peut être courbée ou non linéaire (courbe d’isocoût). Tout au long d’une même droite d’isocoût, le coût total de production reste inchangé malgré les variations des quantités de facteurs utilisées. Plus une droite d’isocoût est éloignée de l’origine, plus elle représente un coût de production élevé ; à l’inverse, les droites plus proches de l’origine correspondent à des coûts plus faibles. Le schéma ci-dessous illustre deux droites d’isocoût : la première est associée à un coût de production C, et la seconde à un coût C', avec C > C'.

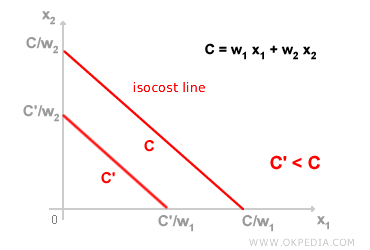
Les points d’intersection des droites d’isocoût avec les axes du graphique indiquent la quantité maximale de chaque facteur de production pouvant être utilisée pour un budget donné. Par exemple, si le coût total est C et que les prix des facteurs X₁ et X₂ sont respectivement w₁ et w₂, alors l’intersection avec l’axe des abscisses est donnée par C/w₁, tandis que celle avec l’axe des ordonnées est C/w₂. La pente de la droite d’isocoût correspond à la valeur absolue du rapport des prix des facteurs, soit w₁ / w₂, et est appelée taux marginal de transformation. L’ensemble des droites d’isocoût, chacune correspondant à un niveau de coût total différent, forme une famille d’isocoûts.