Fonction de production

La fonction de production établit le lien entre la quantité d’un bien produit (output) et les différentes quantités de facteurs de production utilisés. C’est un concept clé en microéconomie, qui permet d’analyser les décisions de production. Mathématiquement, elle exprime comment l’output (Y) d’un bien dépend des intrants (X) utilisés au cours d’une période donnée.

Y = f ( x₁ , x₂, x₃, ... , x_n)

À partir d’un ensemble de production Z, la fonction de production indique le niveau maximal d’output atteignable pour une combinaison donnée d’intrants productifs, en supposant un capital fixe sur une période donnée. Dans le cas le plus simple, où il n’y a qu’un seul bien produit (Y) et un seul facteur de production (X), la fonction de production s’écrit :

Y_q = f ( x_q )

Lorsqu’on étudie un seul intrant et un seul output, la fonction de production peut être représentée graphiquement sur un repère cartésien : l’output (Y) est en ordonnée et la quantité d’intrant (X) en abscisse. Cette représentation est appelée la courbe de production.

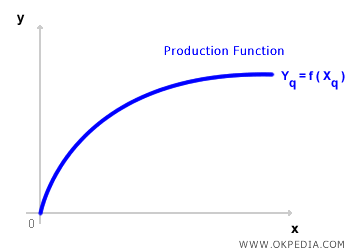
D’un point de vue graphique, la fonction de production correspond à la frontière de l’ensemble de production. Elle représente le processus de production optimal qui maximise l’output (Y) pour chaque niveau d’intrant (X). Mathématiquement, elle possède les propriétés suivantes :

• Continuité : La fonction de production est continue car l’output (Y) et les intrants (X) peuvent varier de manière infinitésimale.
• Monotonie : Elle est monotone, c’est-à-dire qu’une augmentation de la quantité d’intrant (X) ne peut jamais entraîner une diminution de l’output (Y).

La forme de la fonction de production dépend des rendements d’échelle, qui peuvent être décroissants, constants ou croissants :

• Rendements constants : L’output varie dans la même proportion que les intrants.
• Rendements croissants : L’output augmente plus vite que la quantité d’intrants utilisés.
• Rendements décroissants : L’output croît plus lentement que l’utilisation des intrants.

Lorsque les rendements d’échelle sont croissants, la fonction de production adopte la forme suivante :

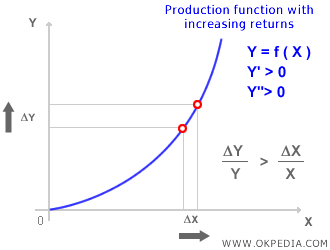
Fonctions homogènes. Une fonction homogène de degré k est un outil utile pour décrire les rendements d’échelle. Le degré d’homogénéité (k) indique le comportement de la fonction :

• k = 1 : Rendements d’échelle constants.
• k > 1 : Rendements d’échelle croissants.
• k < 1 : Rendements d’échelle décroissants.

Fonction de production à court terme. À court terme, la fonction de production illustre la relation entre les intrants et l’output en supposant que le capital et la technologie sont fixes. Autrement dit, elle représente une courbe de production statique. Une entreprise peut ajuster sa production en modifiant la quantité d’intrants variables, comme la main-d’œuvre, mais elle ne peut ni modifier sa capacité de production ni améliorer sa technologie. Ses choix sont donc limités par la frontière de production.

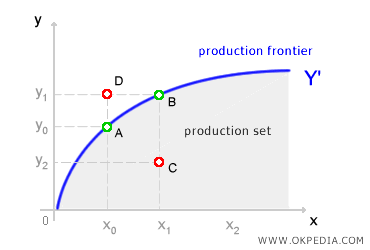
Dans le graphique ci-dessus, les points A et B se situent sur la frontière de production et correspondent à des combinaisons efficaces d’intrants et d’output, car ils maximisent l’output (Y) pour un niveau donné d’intrants (X). En revanche, le point C, bien qu’appartenant à l’ensemble de production, est inefficace puisqu’il génère un output (Y₂) inférieur au maximum atteignable (Y₁) pour la même quantité d’intrant (X₁). Quant au point D, il est inatteignable, car il se situe au-delà de la frontière de production.

Progrès technologique. À long terme, les entreprises peuvent accroître leur capacité de production et adopter de nouvelles technologies, ce qui améliore leur productivité et leur efficacité. Lorsqu’une innovation technologique survient, la fonction de production évolue. Graphiquement, si les progrès permettent d’augmenter l’output pour une même quantité d’intrants, la courbe de production se déplace vers le haut, illustrant une courbe dynamique.

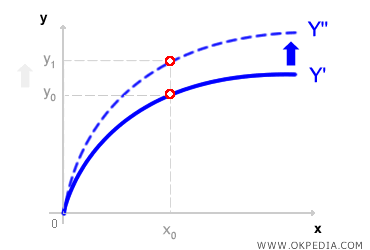
Les innovations technologiques permettent aux entreprises de produire davantage avec la même quantité d’intrants ou, à l’inverse, de réduire l’utilisation des intrants tout en conservant le même niveau d’output, améliorant ainsi leur efficacité productive.