Boîte d'Edgeworth

La boîte d'Edgeworth est un outil graphique qui permet d'analyser la répartition et l'échange de deux biens entre deux agents économiques, ainsi que les conditions d'équilibre dans une économie de pur échange. Cet outil a été introduit pour la première fois par l'économiste britannique Francis Ysidro Edgeworth et a ensuite été perfectionné par A.L. Bowley. La boîte d'Edgeworth peut servir à étudier l'échange de deux biens (X et Y) entre deux agents dans une économie de pur échange (la boîte d'échange d'Edgeworth), ou à analyser l'allocation des facteurs de production (K et L) entre deux entreprises. Dans le premier cas, on utilise des courbes d'indifférence pour représenter les préférences des agents, tandis que dans le second, on se sert de courbes isoquantes pour illustrer la relation entre les facteurs de production.

Boîte d'échange d'Edgeworth

Considérons deux agents économiques (A et B) dotés de biens (X et Y), sans activité de production. La boîte d'Edgeworth permet de déterminer combien de chaque bien sera échangé entre les deux agents, en fonction de leurs dotations initiales et de leurs préférences individuelles.

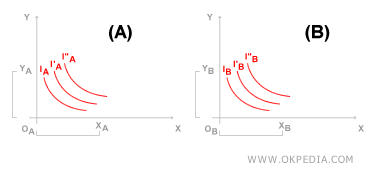
Dans le premier diagramme cartésien (Diagramme A), nous représentons les courbes d'indifférence de l'agent A, qui commence avec une dotation initiale de X_A unités du bien X et de Y_A unités du bien Y. Dans le second diagramme (Diagramme B), nous montrons les courbes d'indifférence de l'agent B, dont la dotation initiale se compose de X_B unités du bien X et de Y_B unités du bien Y.

Construction de la boîte d'Edgeworth

Pour construire la boîte d'Edgeworth, on fait pivoter le diagramme cartésien de l'agent B (Diagramme B) de 180° avant de le superposer au Diagramme A. Le résultat est un graphique rectangulaire avec deux origines. Depuis l'origine située en bas à gauche O_A, nous pouvons mesurer les dotations et les échanges de l'agent A. Depuis l'origine en haut à droite O_B, nous pouvons faire de même pour l'agent B. La boîte d'Edgeworth se présente ainsi :

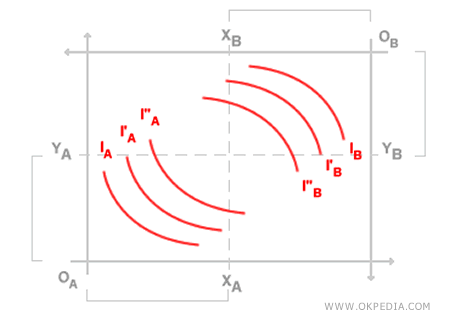
La boîte d'Edgeworth est formée de deux diagrammes cartésiens superposés, où les quantités de biens A et B sont mesurées le long des axes respectifs. La longueur des axes X et Y dans la boîte est déterminée par les dotations totales des deux agents. Par exemple, la longueur de l'axe des X est la somme X_A + X_B, qui représente la quantité totale du bien X détenue par les deux agents. De même, l'axe des Y est défini par la somme Y_A + Y_B, qui représente la quantité totale du bien Y. Les courbes d'indifférence restent convexes en direction de leurs origines respectives.

Par exemple, les courbes d'indifférence I_B de l'agent B sont convexes en direction de l'origine O_B, et l'agent B préfère toujours la courbe d'indifférence extérieure I''_B à la courbe intérieure I'_B. Cette caractéristique de la boîte d'Edgeworth permet d'observer l'évolution des dotations des deux agents pendant le processus d'échange. La boîte d'Edgeworth est un outil graphique essentiel en économie politique et en microéconomie.

Boîte de production d'Edgeworth

Dans la boîte de production d'Edgeworth, les axes cartésiens représentent les quantités des facteurs de production K et L. Les isoquantes sur le plan cartésien indiquent les combinaisons de ces facteurs nécessaires pour produire les biens A et B. La somme K_A + K_B représente la quantité totale de capital (K) disponible sur le marché, tandis que la somme L_A + L_B correspond à la quantité totale de travail (L). En fonction de la technologie de production utilisée par les entreprises (représentée par les isoquantes), les points de tangence entre les courbes isoquantes indiquent l'allocation optimale du capital (K) et du travail (L).

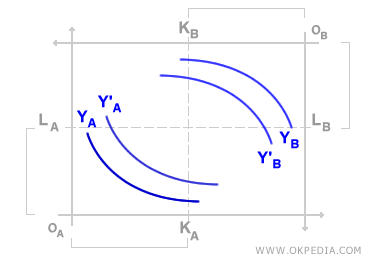
Équilibre dans la boîte d'Edgeworth. L'équilibre dans la boîte d'Edgeworth est atteint aux points où les courbes d'indifférence des deux consommateurs sont tangentes (le point de contrat). À ces points, le taux marginal de substitution entre les biens est identique pour les deux consommateurs. Cet équilibre reflète une situation optimale au sens de Pareto, ce qui signifie qu'aucun consommateur ne peut améliorer son utilité sans diminuer celle de l'autre. L'ensemble des points de tangence entre les courbes d'indifférence constitue ce qu'on appelle la courbe de contrat. De la même manière, l'ensemble des points de tangence entre les isoquantes