Axiome de transitivité

L'axiome de transitivité est un principe fondamental de la théorie des préférences du consommateur : il garantit la cohérence logique des choix. Il stipule que si un consommateur préfère le panier A au panier B, et B au panier C, alors il doit nécessairement préférer A à C. Graphiquement, cet axiome implique que les courbes d’indifférence ne peuvent en aucun cas se croiser ; une telle situation remettrait en cause la logique même des préférences. Le graphique ci-dessous illustre un cas hypothétique où deux courbes d’indifférence se croisent, en lien avec trois paniers de consommation.

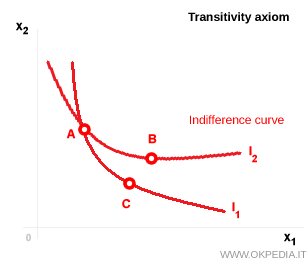
Dans cet exemple, les courbes d’indifférence ne reflètent pas un classement cohérent des préférences. Les paniers A et B se trouvent sur la même courbe $I_2$, ce qui signifie que le consommateur leur attribue le même niveau d’utilité. Il en va de même pour les paniers A et C, tous deux situés sur la courbe $I_1$. D’après l’axiome de transitivité, cette situation devrait impliquer une indifférence entre B et C. Or, ce n’est pas le cas : le panier B est positionné sur une courbe d’indifférence plus élevée que C, ce qui le rend strictement préférable. D’où une contradiction manifeste :

$$ B \succ C \quad A = C \quad A = B $$

Si le consommateur est indifférent entre A et B, et également entre A et C, il ne peut logiquement préférer B à C. C’est précisément ce type d’incohérence que l’axiome de transitivité permet d’exclure dans un modèle rigoureux du comportement du consommateur.