Neutralité au risque

La neutralité au risque décrit l'attitude d'un individu face au risque. Un agent est dit neutre au risque lorsque l'utilité de la valeur monétaire espérée d'une loterie est égale à l'utilité espérée de ses résultats. Autrement dit, étant donnée une loterie (une variable aléatoire) avec deux issues possibles X₁ et X₂, et des probabilités associées p₁ et p₂, la neutralité au risque se traduit par l'équation suivante :

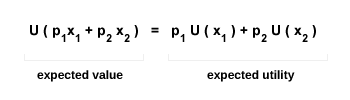
Le membre de gauche représente l'utilité de la valeur espérée de la loterie ; celui de droite, l'utilité espérée des gains. Dans cette configuration, l'individu est indifférent entre percevoir une somme certaine équivalente à la valeur espérée, ou participer à la loterie. Ce comportement peut être illustré à l'aide du diagramme cartésien ci-dessous :

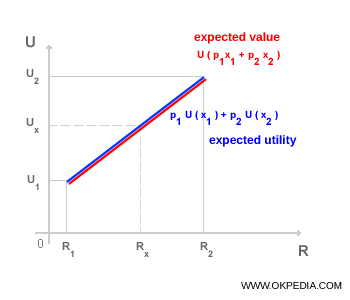
Le graphique met en évidence l'utilité de la valeur espérée (courbe rouge) et la fonction d'utilité espérée (courbe bleue). La coïncidence parfaite des deux courbes indique que l'individu n'éprouve aucune préférence entre un résultat certain et une issue aléatoire ayant la même valeur espérée. En d'autres termes, un agent neutre au risque fonde ses décisions exclusivement sur les résultats monétaires attendus, sans accorder de poids à l'incertitude.

Corollaire. Un individu est neutre au risque si la valeur espérée d'une loterie est égale à son équivalent certain.