Fonction de coût

La fonction de coût établit le lien entre le niveau de production et le coût minimal nécessaire pour l’atteindre. Étant donnée une fonction de production à deux facteurs de production, y = f(x₁, x₂), la fonction de coût détermine la dépense minimale C* permettant de produire un volume donné Y.

C = C(Y)

Graphiquement, le coût minimal correspond au point où une droite d’isocoût est tangente à une courbe d’isoquante (allocation optimale des facteurs). Comme on le sait, les courbes d’isoquantes représentent les différentes combinaisons de facteurs de production (x₁, x₂) permettant d’obtenir un même niveau de production Y. En étudiant un ensemble d’isoquantes, on peut visualiser les niveaux de production associés à une fonction de production. En reliant les points où les isoquantes touchent les droites d’isocoût, on obtient les valeurs (C, Y) qui permettent de tracer la fonction de coût.

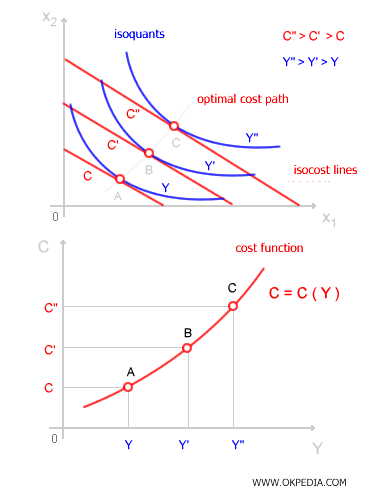
La fonction de coût met en évidence l’évolution du coût total C en fonction du niveau de production Y. Mathématiquement, elle est toujours croissante, ce qui signifie que sa dérivée première est strictement positive.

C'(x) > 0

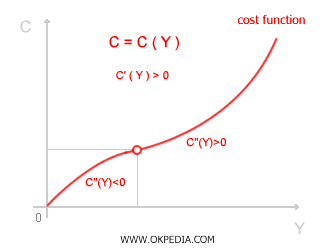
Autrement dit, accroître la production implique nécessairement une consommation plus importante de facteurs de production, ce qui entraîne une augmentation des coûts. Toutefois, le rythme auquel ces coûts augmentent n’est pas constant : il dépend de la dérivée seconde de la fonction de coût C"(x), ainsi que des coûts marginaux et moyens. En général, lorsque Y augmente, la hausse des coûts de production est d’abord modérée (C"(x) < 0), puis s’accélère à partir d’un certain seuil (C"(x) > 0). En d’autres termes, à faible niveau de production, les coûts augmentent lentement, mais au-delà d’un certain point, leur croissance devient plus rapide.

Lors de la construction de la fonction d’isocoût, on suppose que les prix des facteurs restent constants, quel que soit le niveau de production. Dans ce cadre, la dépense totale est directement liée au volume produit Y, et non à la quantité de facteurs achetée. Cette hypothèse est valable lorsque la taille de l’entreprise est insuffisante pour influencer les prix des intrants. Sur un graphique, cela se traduit par des droites d’isocoût dont la pente reste inchangée, quel que soit le niveau de production Y.